Formal Proposal:
APL Array Notation

Note: This proposal's specification for scoping in literal namespaces has been changed based on feedback received after its initial publication. Affected sections are marked by a vertical bar on the left, with removed text struck through and added text underlined.

One of the defining features of the APL language is the ability to denote numeric vectors directly through juxtaposition — separating the elements by spaces, as in 0 1 1 2 3 5 8. The notation for character “vectors” is similar to that for “strings” in most other languages, using quotes to denote the start and end of a list of characters. When generalised arrays were added to the language in the early 1980s, the most popular APL dialects extended the vector notation to allow nested arrays to be written using so-called strand notation, allowing the juxtaposition of sub-expressions producing arrays to form a one-dimensional array — as in (2+2) (FOO 42) MAT

Strand notation works well for small, relatively simple one-dimensional arrays. As soon as arrays are too large to be represented on a single line of code, deeply nested, rank greater than one, or (in APL systems that support them) contain name­spaces or objects, APL requires the use of primitives or system functions to assemble them from simple components.

The flexibility of the APL language has allowed many APL programmers to work around the issue, either by implementing custom array notations or by using the ability of most APL interpreters to simply store arrays within saved workspaces without having an actual source form of the data. Within specific applications, domain specific notations can be very successful, but readability is poor for anyone not trained in the specific variation used — or who is missing the tooling required to interpret them — as well as sometimes having significant run-time cost.

Recently, the need for a better notation for arrays has grown within the Dyalog APL community:

• The switch to text-based sources means that arrays that represent constants, enumerations or initial values — that arguably constitute part of the source of an application — need a textual representation if they are to be managed using the same tools as functions and operators.
• The increased use of name­spaces and name/value pairs as arguments to both user-defined and system functions makes the lack of a good notation for name­spaces painful.

Dyalog Ltd intends to implement core language support for a notation that makes it possible to write most arrays literally, without requiring the use of primitive functions, over multiple lines of source where this increases readability. It can be used to write nested arrays, and arrays of rank greater than one. The notation also describes many name­spaces/objects, providing both inline and anonymous definitions.

Array notations similar to that proposed here are currently supported in some newer implementations such as dzaima/APL and the APL-derivative BQN. Experimental implementations using APL models are available within some tools in the Dyalog eco-system, such as the Link tool which supports the representation of code and data in Unicode text files and the functions Serialise and Deserialise within the name­space ⎕SE.Dyalog.Array. You can also try it out in the interactive online sandbox.

Providing feedback

Dyalog is keen to have feedback from the array language community on the notation proposed here so that we can feel confident about the design, before we proceed with our implementation. Our hope is that we will be able to keep the differences between future array notations within the family of array languages to a minimum.

We will monitor the APL Orchard chatroom, the APL Farm's #apl channel, the r/apl and r/apljk subreddits, and the comp.lang.apl newsgroup for feedback. (See APL Wiki for information about these forums.) In addition, we have created a topic in our own forum. If you prefer not to comment in public, please send comments by e-mail. Dyalog will update the discussion page for APL Wiki's Array notation design considerations article to contain a record of significant feedback.

Overview

The fundamental mechanism underlying the proposed notation is to group multiple lines, or statements separated by the traditional APL statement separator (diamond ⋄), within parentheses and square brackets. Statements within parentheses () represent vectors — roughly equivalent to stranding — while statements within square brackets [] represent higher rank arrays, where the vector is subjected to a Mix. The notation also supports name­spaces or dictionaries, where zero or more statements in the form name:value are collected within parentheses ().

Examples

A very common technique used for array construction in APL is repeated concatenation resulting in the desired value being held in a variable (z in the below examples). Array notation should make it possible to express the complete array directly. In addition, the traditional technique sometimes involves the creation of helper variables as a side effect.

Note that for all Dyalog APL examples, monadic ⊃ is Mix (that is, using ⎕ML←3) for readability outside the Dyalog community.

In the examples below, the traditional method of creating an array is marked Ⓣ, the proposed APL array notation is marked Ⓐ, and the minimal-style boxed display output (as provided by ]disp and disp from the dfns workspace) is marked Ⓑ.

Basic arrays

(0 6 1 8) (1 4 1 4 2) (2 7 1 8 2 8) (3 1 4 1 5)

(0 6 1 8 ⋄ 1 4 1 4 2 ⋄ 2 7 1 8 2 8 ⋄ 3 1 4 1 5)

┌───────┬─────────┬───────────┬─────────┐
│0 6 1 8│1 4 1 4 2│2 7 1 8 2 8│3 1 4 1 5│
└───────┴─────────┴───────────┴─────────┘

z← (0 6 1 8) (1 4 1 4 2)
z,←(2 7 1 8 2 8) (3 1 4 1 5)

(0 6 1 8 ⋄ 1 4 1 4 2
 2 7 1 8 2 8 ⋄ 3 1 4 1 5)

┌───────┬─────────┬───────────┬─────────┐
│0 6 1 8│1 4 1 4 2│2 7 1 8 2 8│3 1 4 1 5│
└───────┴─────────┴───────────┴─────────┘

z← ⊂'Three'
z,←⊂'Blind'
z,←⊂'Mice'

('Three'
 'Blind'
 'Mice')

┌─────┬─────┬────┐
│Three│Blind│Mice│
└─────┴─────┴────┘

z←⍉⍪0 6 1 8
z⍪← 1 4 1 4
z⍪← 2 7 1 8
z⍪← 3 1 4 2

[0 6 1 8
 1 4 1 4
 2 7 1 8
 3 1 4 2]

0 6 1 8
1 4 1 4
2 7 1 8
3 1 4 2

z←⍪⊂'Three'
z⍪←⊂'Blind'
z⍪←⊂'Mice'

[⊂'Three'
 ⊂'Blind'
 ⊂'Mice']

[('Three'⋄)
 ('Blind'⋄)
 ('Mice' ⋄)]

┌─────┐
│Three│
├─────┤
│Blind│
├─────┤
│Mice │
└─────┘

More complex arrays

a←⍉⍪0 0 1
a⍪← 1 0 1
a⍪← 0 1 1
z←,⊂a
a←⍉⍪0 1 1
a⍪← 1 1 0
a⍪← 0 1 0
z,←⊂a
a←⍉⍪0 1 1 1
a⍪← 1 1 1 0
z,←⊂a
a←⍉⍪0 1 1 0
a⍪← 1 0 0 1
a⍪← 0 1 1 0
z,←⊂a

([0 0 1
  1 0 1
  0 1 1]

 [0 1 1
  1 1 0
  0 1 0]

 [0 1 1 1
  1 1 1 0]

 [0 1 1 0
  1 0 0 1
  0 1 1 0])

┌─────┬─────┬───────┬───────┐
│0 0 1│0 1 1│0 1 1 1│0 1 1 0│
│1 0 1│1 1 0│1 1 1 0│1 0 0 1│
│0 1 1│0 1 0│       │0 1 1 0│
└─────┴─────┴───────┴───────┘

z←⍉⍪0 'OK'
z⍪← 1 'WS FULL'
z⍪← 2 'SYNTAX ERROR'
z⍪← 3 'INDEX ERROR'
z⍪← 4 'RANK ERROR'

[0 'OK'
 1 'WS FULL'
 2 'SYNTAX ERROR'
 3 'INDEX ERROR'
 4 'RANK ERROR']

┌─┬────────────┐
│0│OK          │
├─┼────────────┤
│1│WS FULL     │
├─┼────────────┤
│2│SYNTAX ERROR│
├─┼────────────┤
│3│INDEX ERROR │
├─┼────────────┤
│4│RANK ERROR  │
└─┴────────────┘

a←⍉⍪3 1 4
a⍪← 1 5 0

b←⍉⍪2 7 0
b⍪← 2 0 0
z←a,[0.5]b

[[3 1 4
  1 5 0]

 [2 7 0
  2 0 0]]

3 1 4
1 5 0

2 7 0
2 0 0

a←,⊂3 1 4
a,←⊂1 5
a←⊃a
b←,⊂2 7
b,← 2
b←⊃b
z←⊃a b

[[3 1 4
  1 5]

 [2 7
  2]]

3 1 4
1 5 0

2 7 0
2 0 0

z←⍉⍪'fns'  ((0 1)(0.7 0)(0.7 0)×size)
z⍪← 'fnd'  ((0 1)(0   0)(0   0)×size)
z⍪← 'lines'((0 0)(0.7 0)(0.7 0)×size)
z⍪← 'lnd'  ((0 0)(0   0)(0   0)×size)

['fns'  ((0 1 ⋄ 0.7 0 ⋄ 0.7 0)×size)
 'fnd'  ((0 1 ⋄ 0   0 ⋄ 0   0)×size)
 'lines'((0 0 ⋄ 0.7 0 ⋄ 0.7 0)×size)
 'lnd'  ((0 0 ⋄ 0   0 ⋄ 0   0)×size)]

The last of the above examples shows the use of an embedded computation — using multiplication and a reference to an external variable. Although this can be extremely useful within an application, systems can prohibit this when reading external source files, to avoid code injection attacks (in the same way that macros can be disabled when loading text documents and spreadsheets).

Namespaces

In the examples below, the traditional method of creating an object is marked Ⓧ for APLX and Ⓓ for Dyalog APL, while the proposed APL array notation is marked Ⓐ. In addition, the closest JavaScript equivalent is marked Ⓙ.

∇z{}∇

⎕NS⍬

()

{}

⍎¨⎕FX¨('a{' '}')('b{' '}')('c{' '}')

⎕NS¨⍬⍬⍬

()()()

(() ⋄ () ⋄ ())

[{},{},{}]

∇z{
    x←'hello'
}

z←⎕NS⍬
z.x←'hello'

(x:'hello')

{x:'hello'}

∇z{
    x←⊃'hello' 'world'
}

z←⎕NS⍬
z.x←⍉⍪'hello'
z.x⍪← 'world'

(x:['hello'
    'world'])

{x:['hello',
    'world']}

∇a{
    x←⊃'hello' 'world'
}
∇b{
    y
}
z←⎕NEW b
z.y←a

z←⎕NS⍬
z.y←⎕NS⍬
z.y.x←⍉⍪'hello'
z.y.x⍪← 'world'

(y:(x:['hello'
       'world']))

{y:{x:['hello',
       'world']}}

∇z{
    FirstName←'Wolfgang'
    LastName←'Mozart'
    Age←35
}

z←⎕NS⍬
z.FirstName←'Wolfgang'
z.LastName←'Mozart'
z.Age←35

(
    FirstName:'Wolfgang'
    LastName:'Mozart'
    Age:35
)

{
    FirstName:'Wolfgang',
    LastName:'Mozart',
    Age:35
}

Technical specification

The notation consists of syntax that was invalid in every mainstream APL implementation before its introduction, thus causing no issues for backwards compatibility. The added syntax consists of these constructs that are currently SYNTAX ERRORs:

• broken round parentheses/parenthesised name–value pair: (…)
• broken square brackets: […]
• empty round parentheses: ()

where broken means interrupted by one or more statement separators (diamonds ⋄ or line breaks).

• A statement here means a value expression, optionally separated with a colon (:) from a preceding valid APL identifier.
• Empty statements make parentheses and brackets broken, but do not otherwise influence the result.
• A broken round parenthesis creates a name­space if every^* separated statement is a name–value pair; every such pair defines a member of the resulting name­space.
• A parenthesised name–value pair creates a name­space; the pair defines the sole† member of the resulting name­space.
• A broken round parenthesis creates a vector if every^* separated statement is a value expression; every such statement forms an element in the resulting vector.
• A broken square bracket creates an array where every separated statement forms a major cell in the resulting array (equivalent to Mix applied to a vector of these), with scalars interpreted as one-element vectors.^‡
• An empty round parentheses creates a new name­space — equivalent to Dyalog APL’s (⎕NS 0⍴⊂'') or shorthand (⎕NS⍬).
• A name–value pair consists of a valid APL identifier, followed by a colon (:) and a value expression^§.

^* A mixture of name–value pairs and value expressions is an error.

^† Besides for system values like ⎕IO.

^‡ For reasons explained below under Minimum rank of items in square brackets, it is proposed that a minimum rank of 1 is imposed on each cell within square brackets. At the time this document was written, the array notation in dzaima/APL did not implement this rule.

^§ See below under Additional content types in name­spaces for details on values that are not given as value expressions.

Statement separators encapsulated in a direct function/dfn/lambda {} or further contained in array notation do not contribute to a parenthesis or bracket being considered broken. For example, in ({1=⍵:'y' ⋄ 'n'}?2) the ⋄ belongs to the inner function/dfn/lambda curly braces, and therefore cannot affect the surrounding parenthesis.

Formal syntax

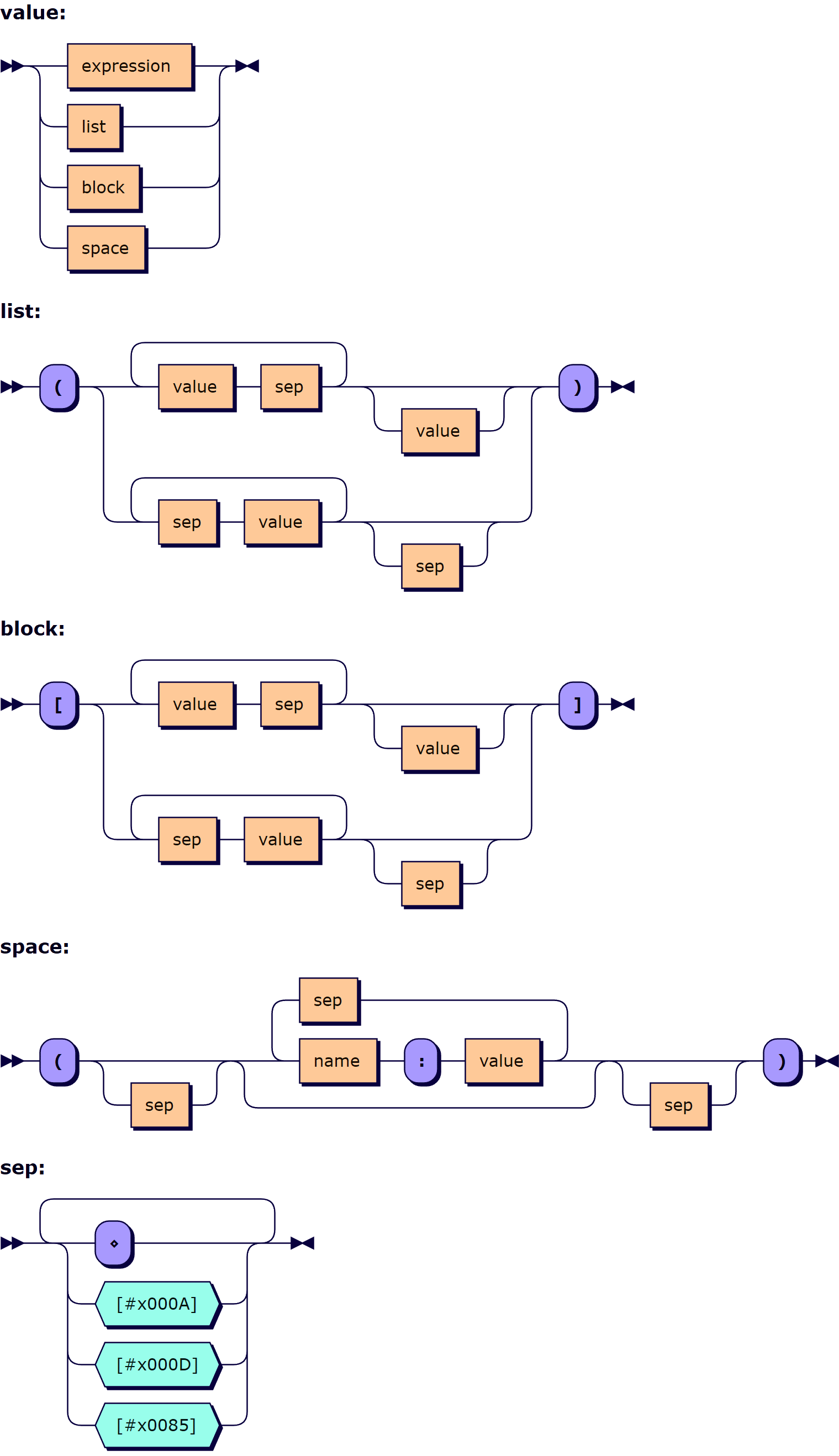
The array notation can be described using Extended Backus–Naur form, where an expression is any traditional APL expression:

value ::= expression | list | block | space
list  ::= '(' ( ( value sep )+ value? | ( sep value )+ sep? ) ')'
block ::= '[' ( ( value sep )+ value? | ( sep value )+ sep? ) ']'
space ::= '(' sep? ( name ':' value ( sep name ':' value )* )? sep? ')'
sep   ::= [⋄#x000A#x000D#x0085]+

The list of sep values is for illustration purposes and is to match the line breaks recognised by the APL implementation. However, these three sep values should be handled when reading Unicode text files.

Syntax diagram

Minimum rank of items in square brackets

As noted above, the proposal suggests that each item within square brackets is coerced to a minimum rank of 1 before assembly of the complete array, while the existing implementation in dzaima/APL allows scalars. The argumentation is purely utilitarian: it is significantly easier to write single-column matrices if vectors are assumed. However, utility (or elegance) is an important design consideration for array notation. Allowing statements in square brackets to have rank 0 provides two ways to denote vectors using parentheses and square brackets.

In the following examples, minimum rank of statements in square brackets is indicated as a circled number, with the traditional method of creating an array marked Ⓣ:

[1
 2]

(1
 2)

(1
 2)

z←,1
z,←2

[[1 ⋄ ]
 [2 ⋄ ]]

[(1 ⋄ )
 (2 ⋄ )]

[1
 2]

z←⍪1
z⍪←2

[⊂'hello'
 ⊂'world']

('hello'
 'world')

('hello'
 'world')

z←,⊂'hello'
z,←⊂'world'

[('hello' ⋄ )
 ('world' ⋄ )]

['hello'
 'world']

z←⍉⍪'hello'
z⍪← 'world']

Scoping in literal namespaces

The authors expect the literal notation for name­spaces to become widely used at runtime. Contrast this with the notation for nested or high rank arrays, which we envision mainly as a mechanism for representing arrays that are part of an application or used during its initialisation.

For use within an application at runtime, the ability to define values in literal name­spaces in terms of already existing names is extremely valuable. Since the name­space is in the process of being created, it will rarely be useful to reference other name­space members. Furthermore, a name­space should be considered unordered, as opposed to Dyalog's existing :namespace … :Endnamespace notation. The latter is often called a script and is executed in order, just like the script for a theatric play. It is proposed that value expressions should be interpreted as if they were running in the surrounding scope. However, one might want to use temporary variables in the creation of such values, and these should not leak out into the surrounding scope.

Therefore, the proposal is that value expressions are evaluated much as expressions in Dyalog dfns; the surrounding scope is visible, but new names that are created become local to the expression, and are not shared between individual value expressions in the same name­space declaration: Any assignments done in a value expression will therefore persist in the surrounding scope:

      long←'bobby'
      short←'jack'
      ns←(short:'jill' ⋄ inner:short∘.=short←3↑long)
      ns.inner
1 0 1
0 1 0
1 0 1
      short     ⍝ unaffected by inner assignment
jack
      ns.short  ⍝ ditto
jill
      short     ⍝ altered by inner assignment
bob
      ns.short  ⍝ unaffected by inner assignment
jill

Additional content types in namespaces

      ns←{
          42∊⍵:100
          (
              dfn:{(+⌿⍵)÷≢⍵}
              tacit:+⌿÷≢
              obj: :namespace
                       val←4
                   :Endnamespace
              tradfn: ∇ (y y)←tradfn y
                      ∇
              recursive: ∇ 42
          )
      } 10
      ns.tradfn ns.recursive
100 100

Note that it is the final ∇ that disambiguates a function definition from a recursive call, as a value can be computed by a recursive call to the surrounding dfn:

      ∇ (y y)←tradfn y
      ∇
      y←42
      ns←{
          42∊⍵:100
          (
              recursive: ∇(y y)←tradfn y
          )
      } 10
      ns.recursive
100

The apparent double naming in tradfn: ∇ (y y)←tradfn y is necessary because a name­space can have a named reference to a function of a different name. Compare the following code which has worked in Dyalog APL for many years:

      ∇ (y y)←tradfn y
      ∇
      ns←⎕NS⍬
      ns.rename←tradfn
      ⎕EX'tradfn'
      ns.rename 100
100 100
      ⎕CR'ns.rename'
 (y y)←tradfn y

Syntactically, this would make it easy to populate a name­space with a reference to a niladic function:

      ns←(
          nilad:∇ r←nilad
                  r←42
                ∇
      )

While it is possible to create such a name­space using current Dyalog APL notation, it requires rather involved code.

Additional considerations

• It would be possible to allow a shorter form when including a tradfn in a name­space under its own name. This could be done by omitting the name: label, making the following two name­spaces equivalent:

  ( tradfn:∇(y y)←tradfn y ∇ )

  ⇔

  ( ∇(y y)←tradfn y ∇ )

• The final decisions on the minimum cell rank within square brackets and the scope of value expressions are still considered open.

A number of other design questions that have been answered in the process of reaching this proposal are preserved on APL Wiki.

Closing remarks

Several people have contributed significant amounts of time to the evolution of an array notation worthy of inclusion as a core component in future APL, adding value to APL notation as a tool of thought. For details, see APL Wiki. We sincerely hope that you will give this proposal your attention and provide feedback.